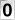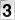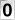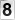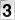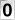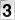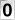5º) MACKENZIE- Dado que:

obter o valor de

a)
b)
c)
d)

RESOLUÇÃO:

6º) EXTRA- Quantos termos tem a Progressão Aritmética (15, 5, ..., -5.005) ?

(A) 5000
(B) 502
(C) 503
(D) 3
(E) 4.

RESOLUÇÃO:

A razao desta PA e r = a₂ – a₁ = 5 – 15 = – 10.

O Termo Geral de uma PA:

E temos que a₁ = 15. Precisamos determinar qual o valor de n para que a_n = -5.005.

Assim:

a_n = a₁+ (n - 1)·r

–5005 = 15 + (n - 1)·(– 10)

–5005 – 15 = (n - 1)·(– 10) ⇔ –5020 = (n - 1)·(– 10) ⇔ ( –5020)/(– 10) = n - 1 ⇔ 5020/10 = n - 1 ⇔ 502 = n - 1 ⇔ 502 + 1= n.

Portanto, n = 503.

7º) EXTRA- Em uma Progressão Aritmética de razão 3 e primeiro termo 2, o vigésimo termo vale:

(A) 60
(B) 59
(C) 58
(D) 57
(E) 56.

Temos que a₁ = 2 e com r = 3, do Termo Geral de uma PA:

Para n = 20, vem que:

a₂₀ = a₁+ (20 - 1)·3 = 2 + (19)·3 = 59

ALBERTIEL RESOLVE 2º SIMULADO PARA O ENEM 2011-2012.

ABRAÇOS E BONS ESTUDOS.