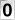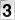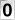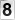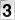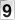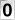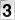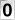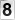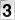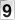1º) EXTRA- O gráfico a seguir ilustra a variação do IPC, Índice de Preços ao Consumidor, no Recife, de abril a agosto de 2005.

Qual a média do IPC nestes cinco meses?
(Aproxime sua resposta até os décimos.)
A) 0,1%
B) 0,2%
C) 0,3%
D) 0,4%
E) 0,5%
RESOLUÇÃO:
A media dos valores do IPC e de (0,7 + 1,59 + 0,31 + 0,25 – 1,17)/5 = 0,336%
2º) EXTRA- O maior número real que satisfaz a equação x3 + 4x2 – x – 4 = 0 é:
(A) 4.
(B) 2.
(C) -1.
(D) -4.
(E) 1.
RESOLUÇÃO:
| x3 + 4x2 – x – 4 = 0 |
Equação dada. |
| x2·(x + 4) – 1·(x + 4) = 0 |
Agrupamos os termos. |
| (x + 4)·(x2 – 1) = 0 |
Colocamos em evidência (x + 4). |
| (x + 4)·(x – 1)·(x + 1)= 0 |
Uma vez que (x2 – 1) = (x – 1)(x + 1). |
|
x + 4 = 0 ⇔ x = – 4
x – 1 = 0 ⇔ x = 1
x + 1 = 0 ⇔ x = – 1
|
Igualando cada fator a zero. |
O maior numero real que satisfaz a equação dada é 1.
3º) EXTRA- Na figura abaixo tem-se o quadrado ABCD, cujo lado mede 30cm. As retas verticais dividem os lados AB e CD em 6 partes iguais; as retas horizontais dividem os lados AD e BC em 4 partes iguais.

Considere o maior número possível de círculos que podem ser construídos com centros nos pontos assinalados, raios medindo 5cm e sem pontos internos comuns. Se do quadrado forem retirados todos esses círculos, a área da região remanescente, em centímetros quadrados, será igual a
a) 150·(6 -  )
)
b) 160·(4 -  )
)
c) 180·(5 -  )
)
d) 180·(4 -  )
)
e) 300·(3 -  )
)
RESOLUÇÃO:
Nas condicões estipuladas, sao 6 circulos conforme a figura:

A area da regiao pedida, em cm2, e 302–6 52 = 150·(6–
52 = 150·(6– )
)
4º) PUC- Em uma Progressão Aritmética, em que o septuagésimo termo é 300 e o octingentésimo termo é 400, a razão desta PA vale:
(A) 10/73
(B) -10/73
(C) 5/76
(D) 1/800
(E) 1/70.
RESOLUÇÃO:
Septuagesimo e o 70° termo e octingentesimo e o 800° termo.
Temos que a70 = 300 e com a800 = 400, do Termo Geral de uma PA:
Assim
a800 = a70+ (800 - 70)·r
400 = 300 + (730)·r
400 - 300 = (730)·r
100 = 730·r ⇔ r = 100/730 = 10/73